PRESSIONS
Loi fondamentale de l'hydrostatique
______________________________________________________
Définition de la " FORCE D'APPLICATION "
Dans l'atmosphère terrestre, tous les corps sont attirés vers le centre de la terre :
c'est la "gravité".
Lorsqu'un corps attiré par cette gravité est en appui sur une surface "statique" ( immobile ), il
exerce une force sur cette surface d'appui. Cette force dépend de la masse "m" de ce corps
et de l'accélération de pesanteur "g" provoquée par l'attraction
terrestre.
La force est une grandeur physique représentée par la lettre majuscule "F".
Son unité est le "Newton".
On peut donc déterminer la force exercée par un corps, à l'aide de la formule :
F = m x g
La masse s'exprime en kilogrammes ( kg ) et l'accélération de
pesanteur en mètres par seconde carré ( m / s² ).
La masse d'un corps ne varie pas.
L'accélération de pesanteur peut varier en fonction de la latitude du globe et de l'altitude.
En France, les physiciens aiment prendre comme référence g = 9,81 m / s² , valeur qui correspond à l'accélération de pesanteur à PARIS.
| Position par rapport à la latitude | g ( m / s² ) |
| Pôles | 9,83 |
| PARIS | 9,81 |
| Equateur | 9,78 |
Mais dans le milieu professionnel, il est souvent d'usage de prendre g = 10 m / s², afin de simplifier les calculs.
NOUS RETIENDRONS DONC : g = 10 m / s²
AINSI, un corps de 20 kilogrammes exercera une force de 200 Newtons sur le sol :
F = m x g = 20 x 10 = 200 N
______________________________________________________
La PRESSION, qu'est-ce que c'est ?
La pression, c'est l'intensité exercée par une force.
Essayez de marcher dans la neige en chaussures ou d'avancer avec des skis.
Vous vous enfoncez en chaussures ...

Source PIXABAY
... beaucoup moins avec les skis

Source PIXABAY
Pourtant, les chaussures de skis et les skis sont sans aucun doute plus lourds que vos chaussures seules.
Mais la surface d'appui a tellement été augmentée par les skis que la pression que vous
exercez sur la neige est bien plus faible.
Deux corps de même masse n'exercent pas toujours la même pression.
Le corps le plus léger peut même exercer une pression plus forte. Pour cela, il suffit que sa surface d'appui soit considérablement réduite par rapport à celle de l'autre corps.
La pression s'exprime par la lettre minuscule " p " ( pour ne pas la confondre avec la puissance qui utilise déjà la lettre majuscule " P " ).
Son unité officielle est le " Pascal ".
On peut donc définir la pression
comme le rapport entre la force exercée par un corps ET sa surface d'application :
p = F / S
avec p : pression, en " Pascals " ( Pa )
F : force, en " Newtons " ( N )
S : surface d'application, en " mètres carrés " ( m² )
______________________________________________________________________________________
EXERCICE 1 : Calculons la pression exercée par l'eau au fond de chaque réservoir

Prenez un brouillon, et commencez par calculer :
1- leur surface d'appui sur le sol : Surface d'appui = Longueur x largeur
2- leur volume d'eau : Volume = Surface x hauteur
3- leur masse d'eau ( m = ρ x V avec ρ eau = 1 000 kg / m3 )
Nous connaissons maintenant la surface d'appui sur le sol et la masse d'eau contenue dans chacun des réservoirs.

Prenez à nouveau votre brouillon, et calculez enfin pour chaque réservoir :
4- la force exercée par l'eau sur le sol : F = m x g avec g = 10 m / s²
5- la pression exercée par le réservoir sur le sol : p = F ÷ S
_______________________________________________________________________________________
INTERPRÉTATIONS DES RÉSULTATS :

Réservoir 3 : deux fois plus d'eau que réservoir 1, mais pression identique en fond de réservoir
Même hauteur d'eau
Réservoir 2 : Même masse d'eau que réservoir 3, mais deux fois plus de pression
car deux fois plus de hauteur d'eau
Réservoir 4 : Beaucoup moins d'eau que réservoir 3, mais quatre fois plus de pression
car quatre fois plus de hauteur d'eau
La masse d'eau contenue dans les réservoirs n'a pas de réelle importance.
Par contre, la pression est proportionnelle à la hauteur d'eau.
______________________________________________________
ORDRE DE GRANDEUR
En prenant g = 10 m / s²,
1 Newton correspond à la force exercée par une masse de 100 grammes,
1 Pascal correspond à la force exercée par une masse de 100 grammes
répartie sur une surface de 1 m².
1 Pascal, c'est à peine plus que la pression exercée
par une feuille de papier posée sur un bureau.
En papeterie, on exprime la qualité du papier en grammes par mètre carré.
Le papier standard pour imprimante est du 80 g / m².
Une feuille de 80 g / m² posée sur un bureau exerce une pression de 0,8 Pa
Le " Pascal " est une unité trop petite pour exprimer la pression de
l'eau dans une installation de chauffage central.
On préfère utilisé le " bar " ( b ) ou le "mètre
de colonne d'eau " ( mCE ) :

ou plus facile à retenir :

Si nous reprenons nos quatre réservoirs, cela donne :

Il est maintenant très facile de faire le lien
entre la HAUTEUR D'EAU et la pression exprimée en mètres de colonne d'eau ( mCE )
______________________________________________________
______________________________________________________
LOI FONDAMENTALE DE L'HYDROSTATIQUE
Cette loi permet de déterminer la différence de pression entre deux points 1 et 2 situés à des hauteurs différentes.
p2 - p1 = - ρ x g x ( h2 - h1 )
avec p2 : pression du fluide au point 2, en Pascals ( Pa )
p1 : pression du fluide au point 1
ρ ( rhô ) : masse volumique du fluide, en kg / m3
g : accélération de pesanteur, en mètres par seconde carré ( m / s² )
h2 : hauteur du point 2, en mètres
h1 : hauteur du point 1, en mètres
______________________________________________________________________________________
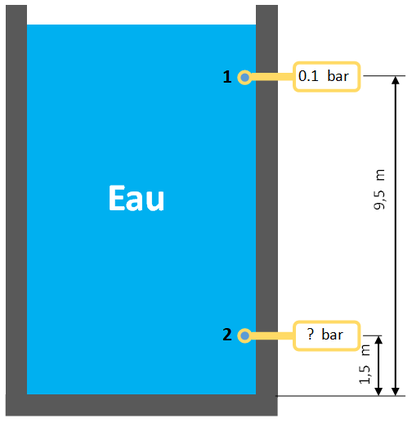
EXEMPLE : Prenons une cuve remplie de fioul et une seconde cuve remplie d'eau.
Appliquons cette loi pour calculer la pression au point 2 dans chaque cuve.
Masse volumique des fluides : ρ eau = 1 000 kg / m3 ρ fioul = 840 kg / m3

CUVE FIOUL :
p2 - p1 = - ρ x g x ( h2 - h1 )
p2 - p1 = - 840 x 10 x ( 1,5 - 9,5 )
p2 - p1 = - 8 400 x ( - 8 ) = 67 200 Pa
p1 = 0,1 bar = 10 000 Pa
p2 = 67 200 + p1 = 67 200 + 10 000
p2 = 77 200 Pa = 0,772 bar
p2 = 0,772 bar
__________________________________________
CUVE EAU :
Faites vous-même le calcul
EXEMPLE 2 : Nous pouvons aussi calculer une hauteur en mesurant la pression en 2 points de la cuve.


CUVE FIOUL :
p1 = 0,5 bar = 50 000 Pa
p2 = 1,5 bar = 150 000 Pa
p2 - p1 = - ρ x g x ( h2 - h1 )
donc ( h2 - h1 ) = ( p2 - p1 ) ÷ ( - ρ x g )
h2 - h1 = ( 150 000 - 50 000 ) ÷ ( - 840 x 10 )
h2 - h1 = - 11,90 m
h1 - h2 = 11,9 mètres
__________________________________________
CUVE EAU :
Faites vous-même le calcul
__________________________________________________________________________
N. B. : Pour le réservoir d'eau, une différence de hauteur de 15 mètres
correspond à une différence de pression de 1,5 bar.
La pression de 1,5 bar peut être convertie très facilement en mètres de colonne d'eau
1,5 bars = 15 mCE
Pour le réservoir de fioul, c'est plus compliqué. Sa masse volumique de 840 kg / m3 empêche toute simplification.
REMARQUE : En bureau d'étude, lorsque les calculs requièrent plus de précision,
on prend g = 9,81 m / s², ce qui donne :
1 bar = 100 000 Pa = 10,19 mCE pour l'eau
et 1 bar = 100 000 Pa = 12,13 mCF ( mètre de colonne de fioul )
______________________________________________________
______________________________________________________
APPLICATIONS aux CIRCUITS de CHAUFFAGE
SIMPLIFICATION :
Dans une installation de chauffage centrale remplie d'eau,
on admet qu'une différence de hauteur de 1 mètre entre deux points du circuit
correspond une différence de pression de 0,1 bar.
ET INVERSEMENT, une différence de pression de 1 bar entre deux points du circuit
correspond à une différence de niveau de 10 mètres

______________________________________________________________________________________
EXERCICE 2 :
Retrouvez la pression que doit indiquer chaque manomètre.
______________________________________________________
______________________________________________________


